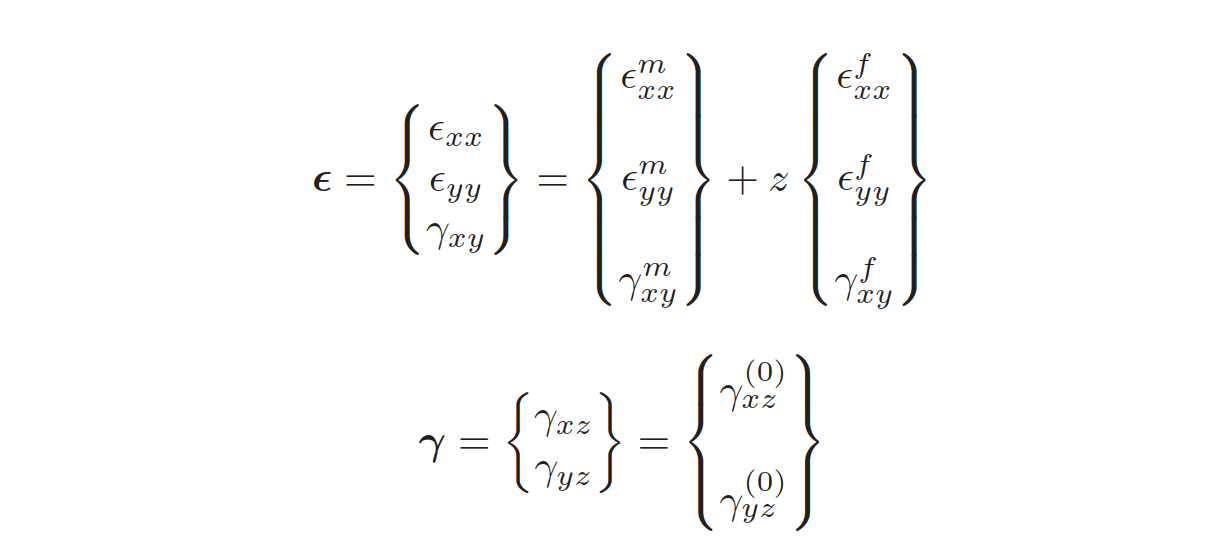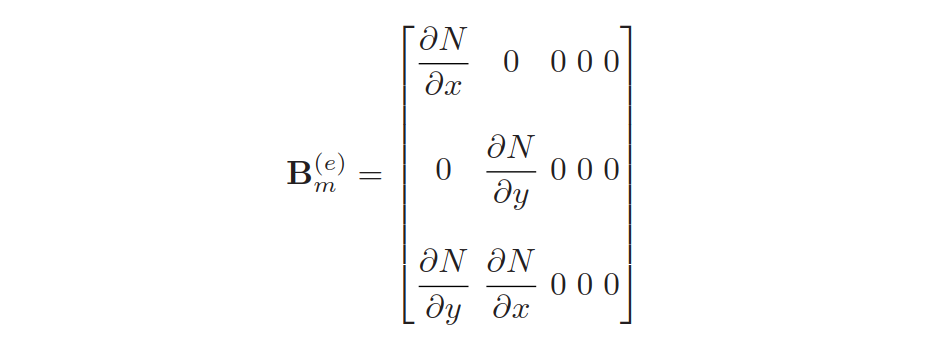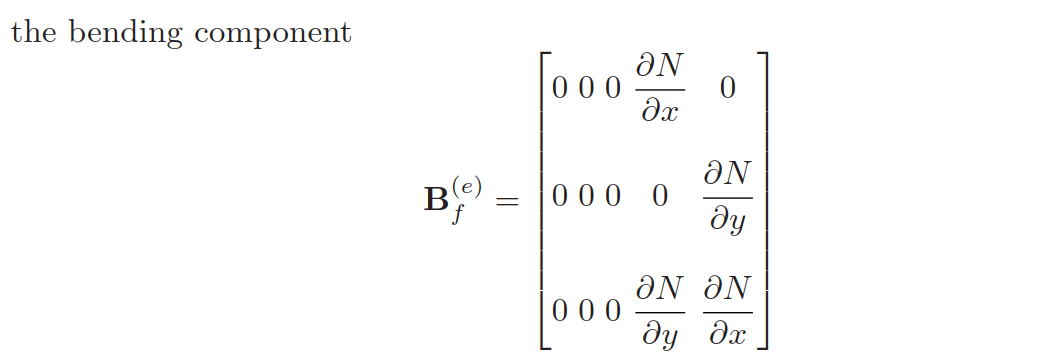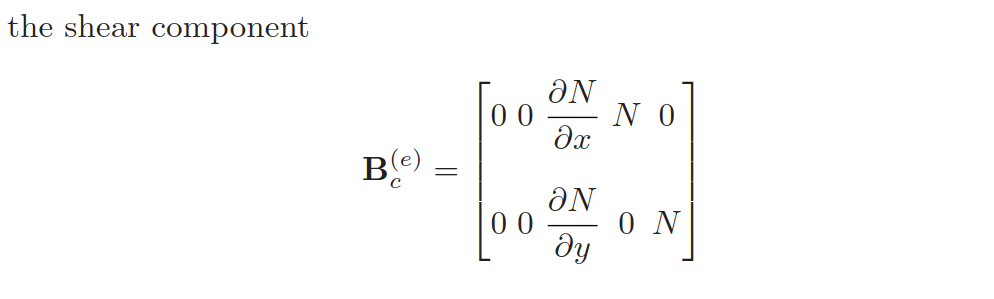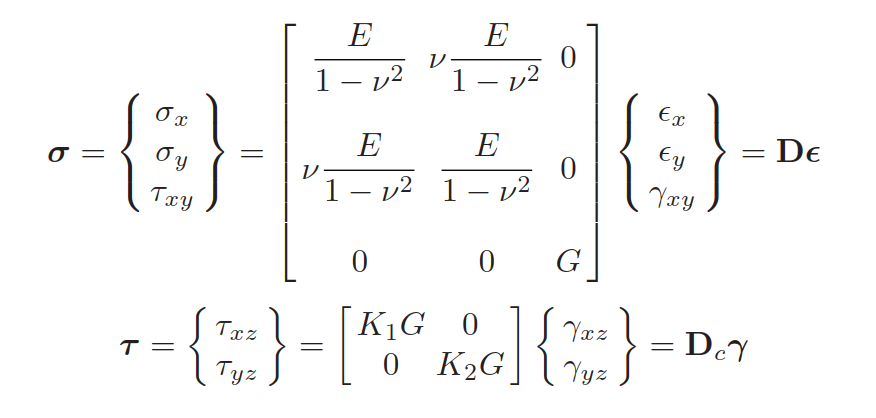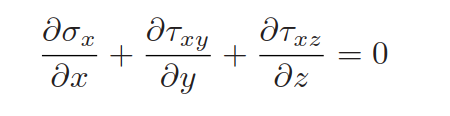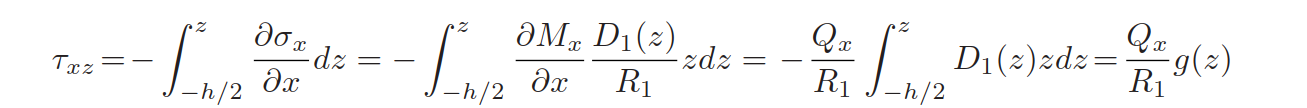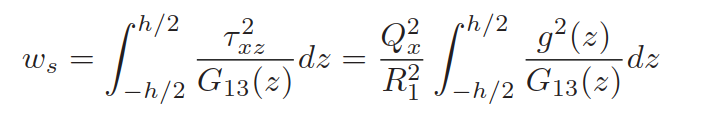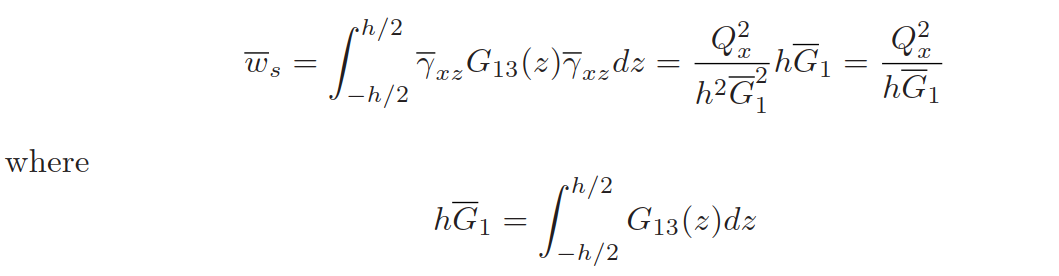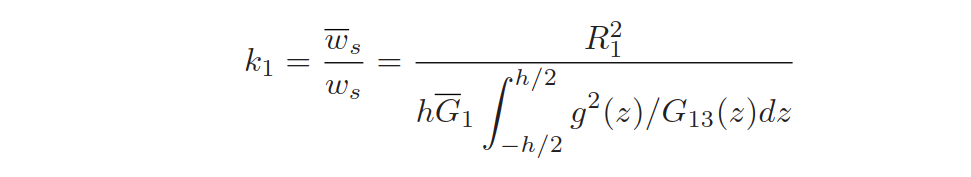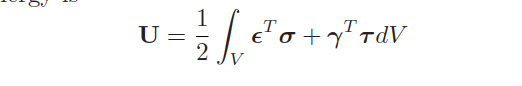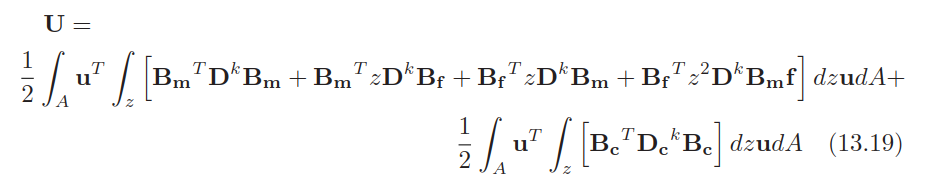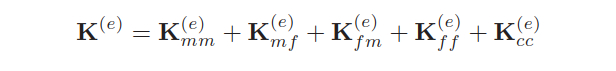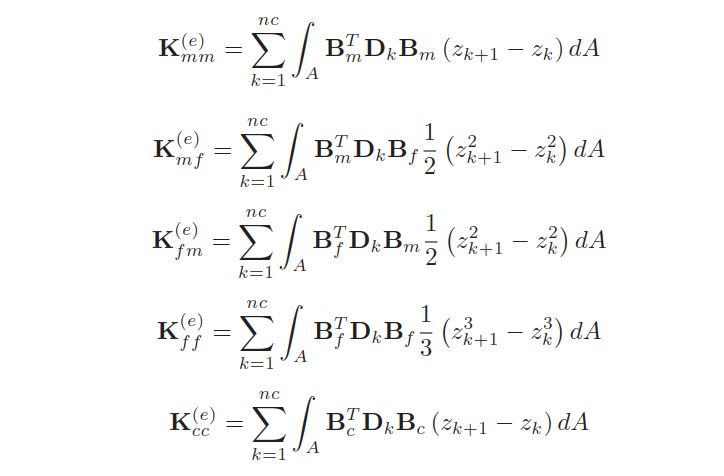Note_Fem_层合板单元格式
推导基于first order shear deformation theory 的层合板单元.给出刚度矩阵、质量矩阵.
假设位移场:
\[\begin{aligned} {{u ( x, y, z )}} & {{} {{} {}=u_{0} ( x, y )+z \theta_{x} ( x, y )}} \\ {{v ( x, y, z )}} & {{} {{} {}=v_{0} ( x, y )+z \theta_{y} ( x, y )}} \\ {{w ( x, y, z )}} & {{} {{}=w_{0} ( x, y )}} \\ \end{aligned} \]
因此,应变和应力表达式为:
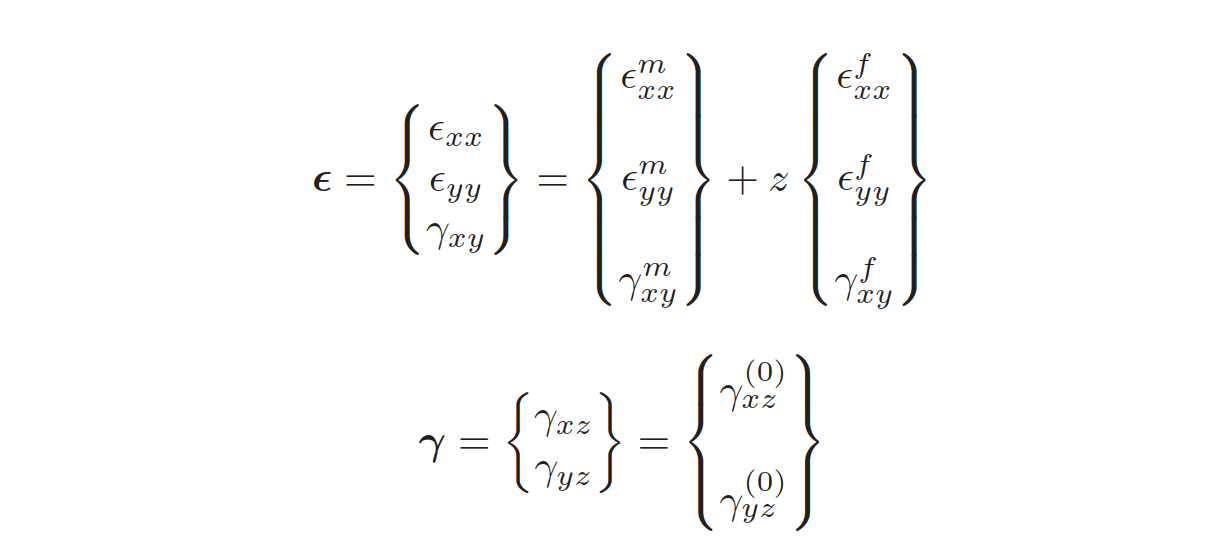
其中:
\[
\left\{\begin{matrix} {{\epsilon_{x, x}^{m}}} \\ {{\epsilon_{y y}^{m}}} \\ {{\gamma_{x y}^{m}}} \\ \end{matrix} \right\}=\left\{\begin{matrix} {{\frac{\partial u_{0}} {\partial x}}} \\ {{\frac{\partial v_{0}} {\partial y}}} \\ {{\frac{\partial u_{0}} {\partial y}+\frac{\partial v_{0}} {\partial x}}} \\ \end{matrix} \right\}
\]
\[
\left\{\begin{matrix} {{\epsilon_{x x}^{f}}} \\ {{\epsilon_{y y}^{f}}} \\ {{\gamma_{x y}^{f}}} \\ \end{matrix} \right\}=\left\{\begin{matrix} {{\frac{\partial\theta_{x}} {\partial x}}} \\ {{\frac{\partial\theta_{y}} {\partial y}}} \\ {{\frac{\partial\theta_{x}} {\partial y}+\frac{\partial\theta_{y}} {\partial x}}} \\ \end{matrix} \right\}
\]
\[
\left\{\begin{aligned} {{\gamma_{x z}^{( 0 )}}} \\ {{\gamma_{y z}^{( 0 )}}} \\ \end{aligned} \right\}=\left\{\begin{aligned} {{\frac{\partial w_{0}} {\partial x}+\theta_{x}}} \\ {{\frac{\partial w_{0}} {\partial y}+\theta_{y}}} \\ \end{aligned} \right\}
\]
应变-位移矩阵B是由三部分(膜+弯曲+剪切)组成的;
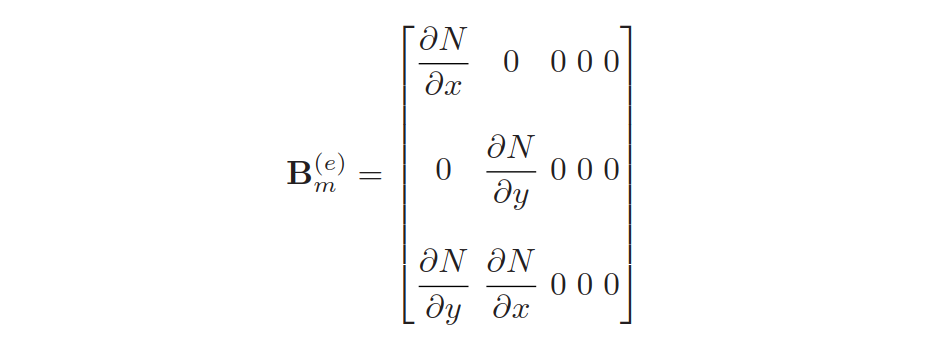
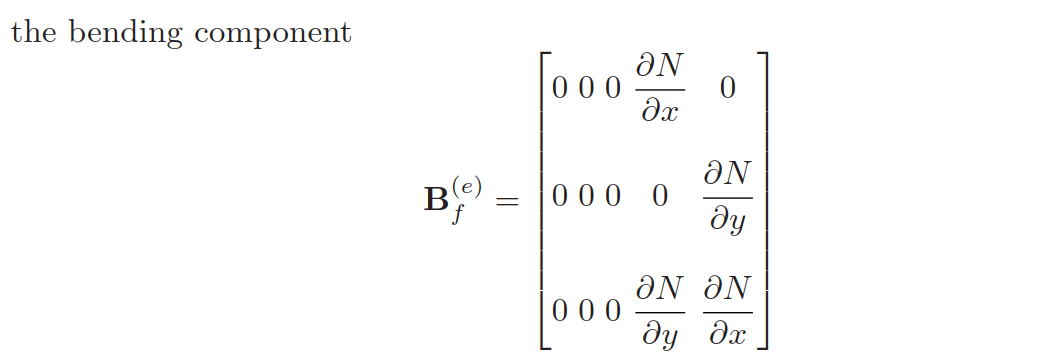
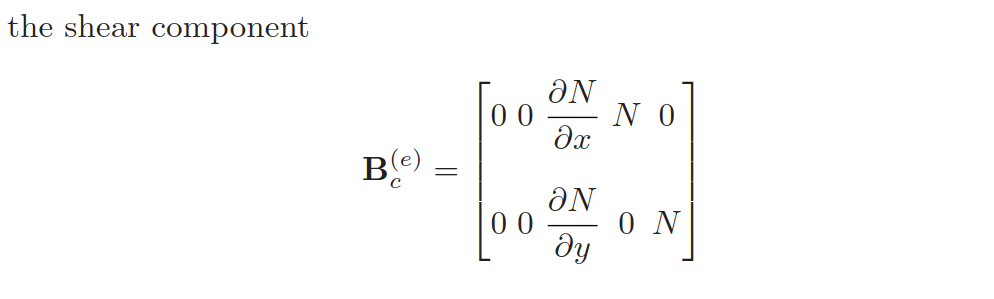
应力-应变关系表达式为(假设法向应力\(\sigma_z=0\)):
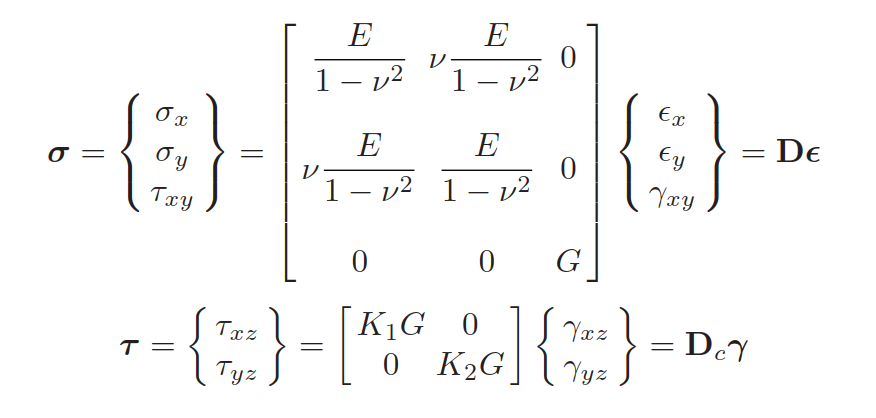
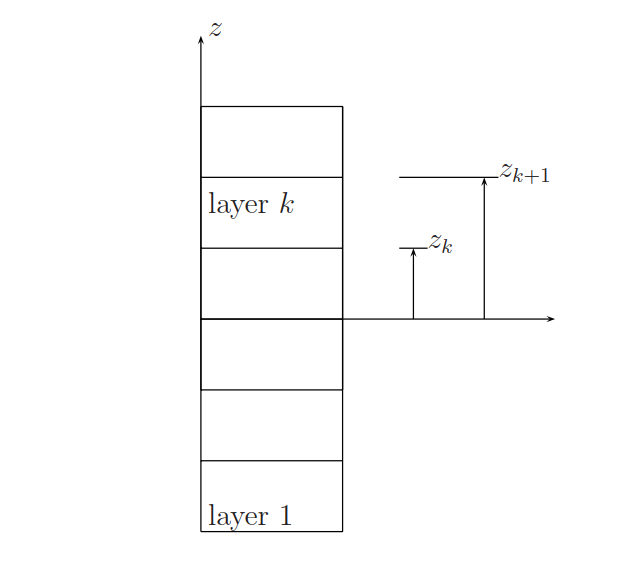
其中,K1,K2是剪切修正系数.在layer 和layer之间的interface,横向剪切应力的连续性需要得到保证.x-方向的平衡方程为:
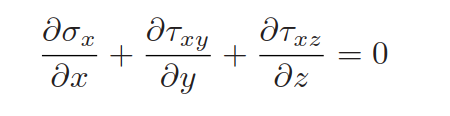
弯曲方向进行积分得到\(\tau_{xz}\):
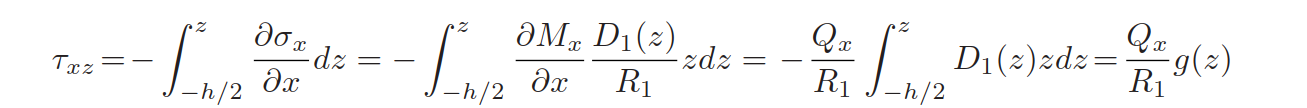
其中:
- \(z\)是厚度坐标
- \(Q_x\): xz-平面的剪切力
- \(R_1=\int_{-0.5h}^{0.5h}D_1(z)z^2dz\):是x方向的plate stiffness
- \(g(z)=-\int_{-0.5h}^zD_1(z)zdz\)是shear shape;
\(g(z)\)将剪切应力图变为抛物线,对于均质截面;\(g(z)=[D_1h^2/8][1-4(z/h)^2]\),应变能为(\(\int_{V}\tau_{xz}*\gamma_{xz}dv\)):
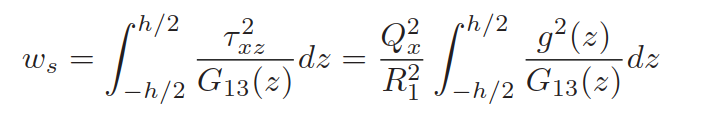
其中\(G_{13}(z)\)是xz平面的横向剪切模量;对于常横向剪切应变来说,应变能为:
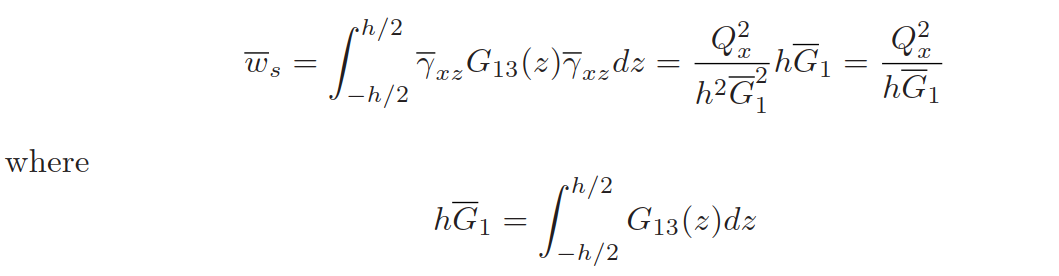
其中,\(\bar{\gamma}_{xz}\)是横向剪切应变的平均值;此时剪切修正系数K1可得:
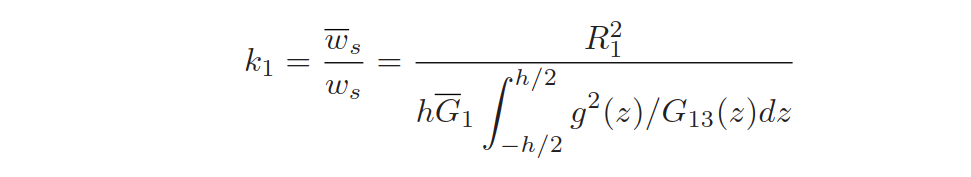
同样的,K2可以用类似的方法求得[1]
K1,K2的取值参考下图,可以取5/6或2/3
参见:1.15 Linear and Nonlinear Elastic Behavior of Multidirectional Laminates

z坐标的排布如下图:
单元应变能为:
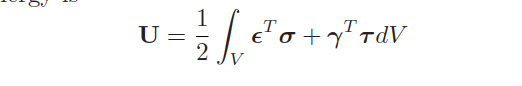
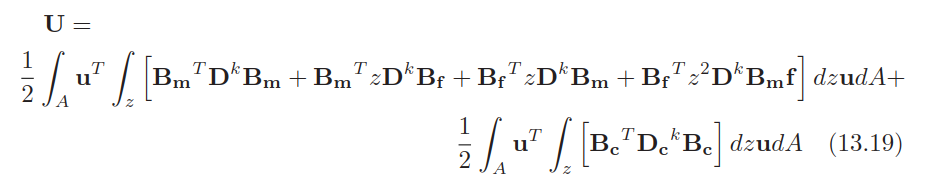
刚度矩阵可以分解为多个部分,包括膜-弯曲耦合;
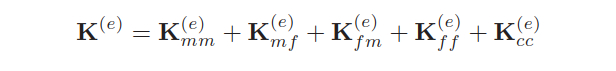
其中:
+ \(K_{mm}^{(e)}\)为表示膜行为部分的刚度阵;
+ \(K_{mf}^{(e)}、K_{fm}^{(e)}\)为表示膜-弯曲耦合行为的刚度阵;
+ \(K_{ff}^{(e)}\)为表示纯弯曲行为的刚度阵;
+ \(K_{cc}^{(e)}\)为表示纯剪切行为的刚度阵;
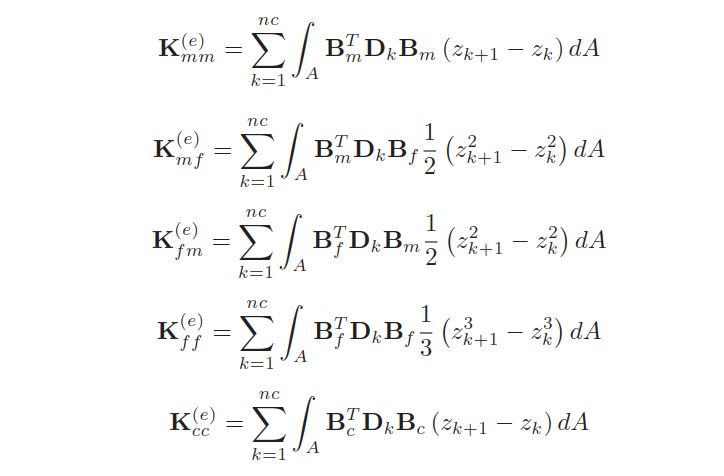
其中\(nc\)是layer number
参考资料:
+ [1] J. A. Figueiras. Ultimate load analysis of anisotropic and reinforced concrete plates and shells. University of Wales, Swansea, 1983.