Note_Fem_Mindlin板Q4单元推导

The Mindlin plate theory 考虑了横向剪切应变的影响[1];具体理论看其他参考书

Mindlin板的应变能为:

单元位移假设: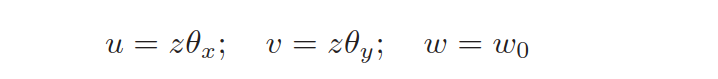

弯曲应变定义为:

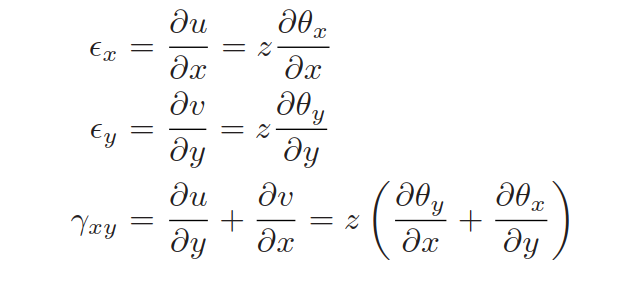
横向剪切应变定义:

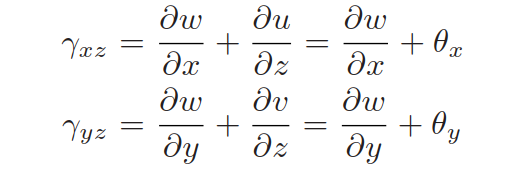
对于均质平板,应力应变关系为:

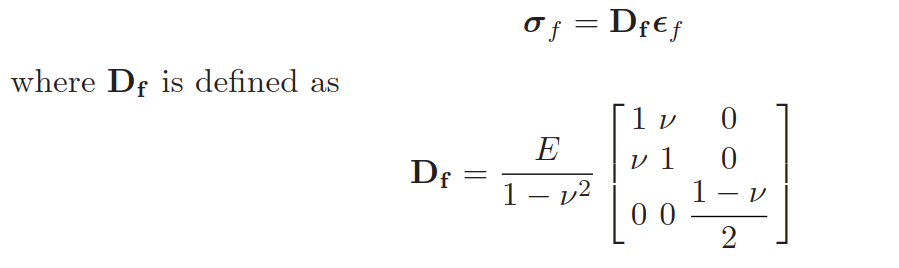
横向剪切应力为(G是剪切模量):

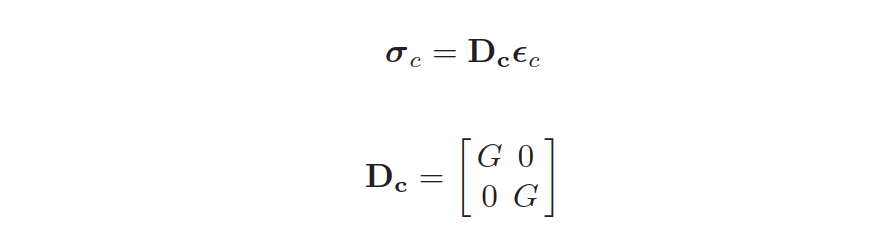
单元离散

单元类型使用双线性四节点的等参单元Q4,则节点自由度个数取3(\(w,\theta_x,\theta_y\)),使用节点自由度插值得到单元位移场:

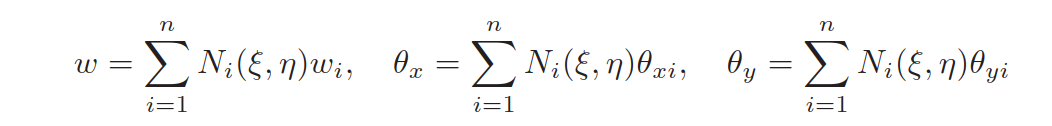
单元自由度向量(12x1)为:

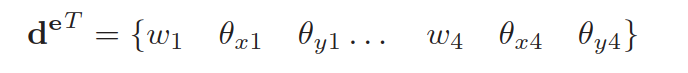
由此,应变的矩阵形式为:

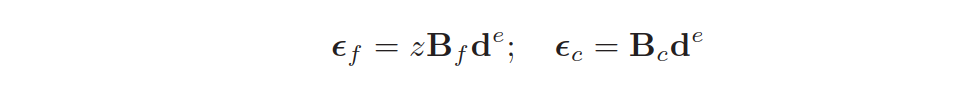
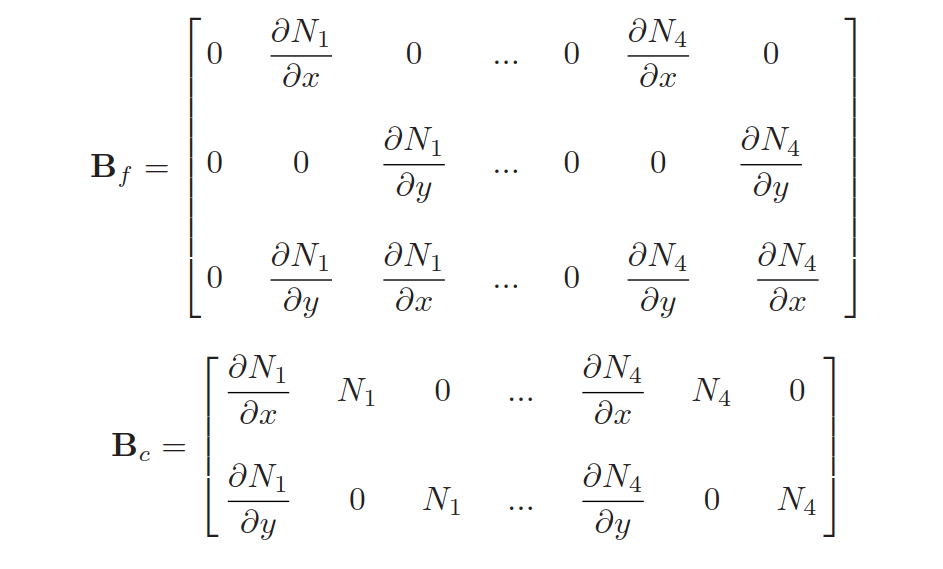
进一步的,平板的应变能为:

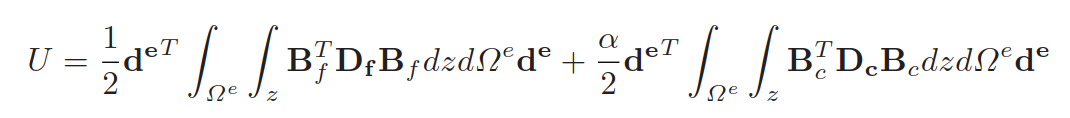
因此,单元刚度矩阵为:

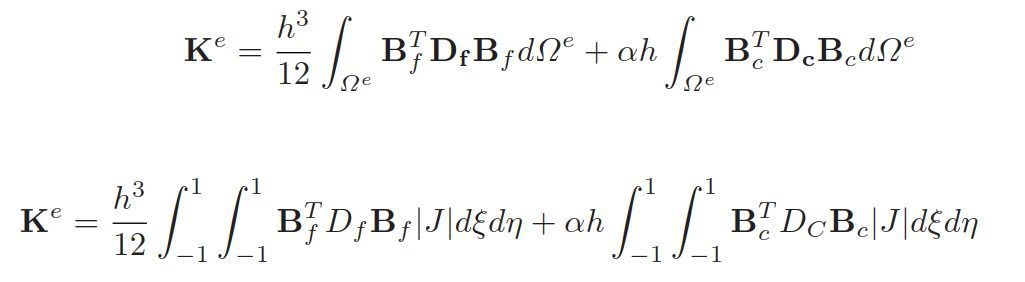
与此同时,分布压力P的等效节点力计算公式为:

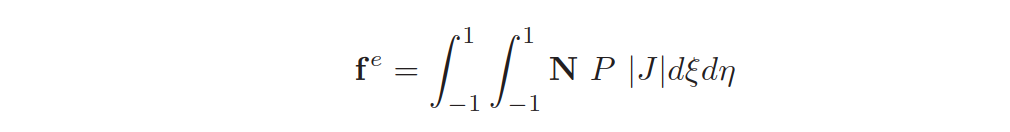
需要注意的是,在使用数值积分求解刚度矩阵时,可以使用2x2高斯积分分点计算弯曲部分的刚度Kf,而使用1高斯计分点计算横向剪切部分的刚度Kc,选择性的高斯积分是减小单元剪切闭锁的一个补救措施[2][3]

单元质量矩阵为

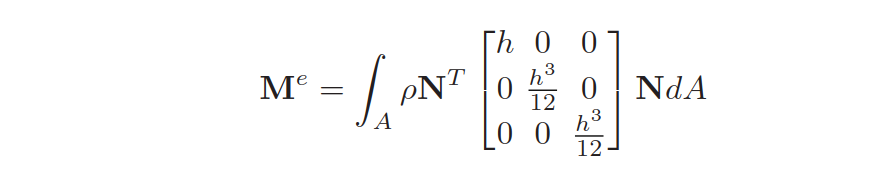
参考资料: + [1]. N. Reddy. Mechanics of laminated composite plates. CRC Press, New York, 1997. + [2] J. N. Reddy. An introduction to the ﬁnite element method. McGraw-Hill, New York,1993. + [3] K. J. Bathe. Finite element procedures in engineering analysis. Prentice-Hall, Engle-wood Cliﬀs, NJ, 1982